Pulp Quality Modelling Using Bayesian Mixture Density Neural Networks

Roland Orre and Anders Lansner.

Abstract

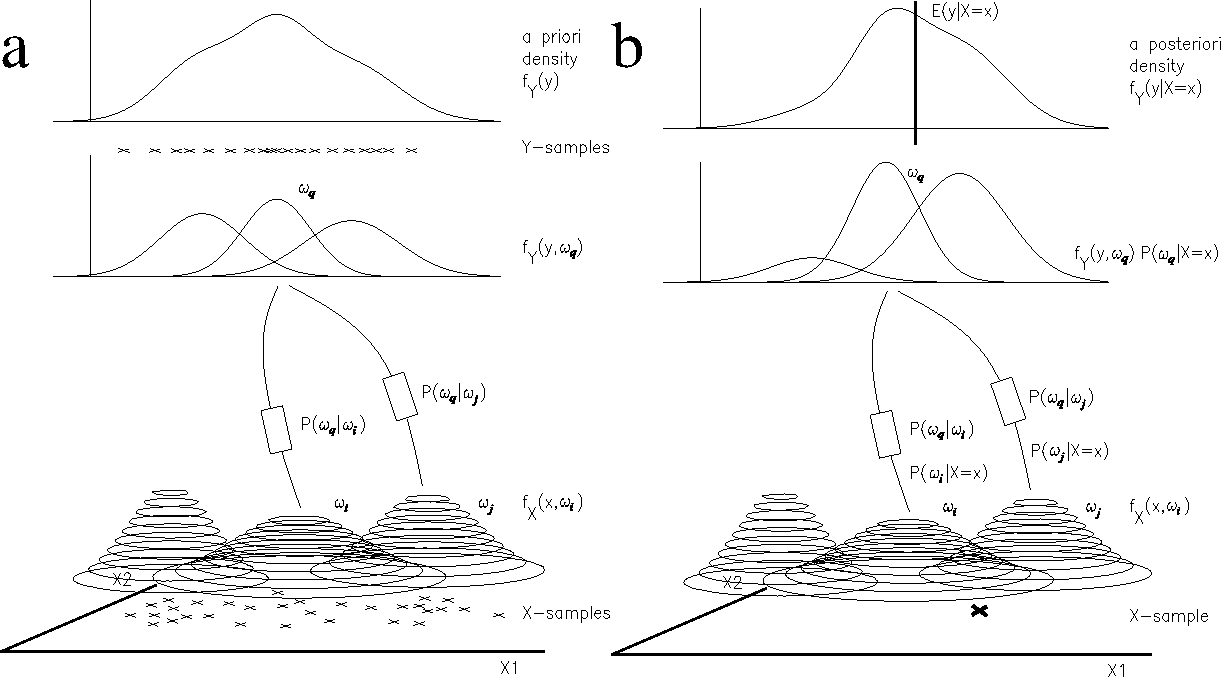
We model a part of a process in pulp to paper production using Bayesian mixture density networks. A set of parameters measuring pulp quality is predicted from a set of process values. The values being predicted are results from time consuming laboratory experiments. In most regression models, like the error backpropagation network, the output is a real value but in this mixture density model the output is an approximation of the density function for a response variable conditioned by a certain explanatory variable value, i.e., f_Y(y|X=x). This density function gives information about the confidence interval for the predicted value as well as modality of the density. Explanatory and response variable spaces are represented by Gaussian RBF:s (Radial Basis Functions) using the stochastic EM (Expectation Maximization) algorithm for calculation of positions and variances. These RBF:s or (density functions) model the a priori density for each variable space. Bayesian associative connections are used to generate the response variable a posteriori density when it is conditioned by an explanatory variable value. We found that this method for function approximation performs comparably well with the best backpropagation network we could find on the same pulp and paper data. It is also straight forward to use with just two design parameters, the number of units which code the explanatory and response variables respectively.